Hike News
Hike News

基本数据结构介绍了解

数据结构 本文总阅读量次

数据结构：反应数据之间的关系，物理或逻辑上的关系。

有两个角度看数据结构：逻辑结构和存储结构。逻辑结构是指数据之间的逻辑关系，有没有联系。而存储结构才是重点，数据怎么存？存成什么样？有顺序、链式、散列存储等，不过主要研究顺序和链式存储等方式，并对他们的运算进行了解。什么是顺序和链式？其实不难理解，就是容易忘(滑稽)！两者都要从逻辑和存储上看。

顺序结构：逻辑上是连续的，即可以通过任意一节点元素找到该数据元素；存储上，就是物理地址是也是相邻的，连在一块。比如顺序表。

链式结构：逻辑上同理；但是物理存储地址却不是连在一块的。比如线性链表。

那不是还有线性和非线性结构吗？这个是什么角度呢？从数据的存储方式看，分为线性和非线性。线性结构或者叫线性表，指一个数据结构中的每个节点最多有一个前驱或后继(指向作用)，则为线性表，可以看作连续线状结构。非空的线性表有以下特征：

  • 只有一个前节点，或头节点，无前件。
  • 只有一个尾节点，无后件
  • 其他节点只有一个前件和后件

那么常见的线性表有这么几个：数组、栈、队列、线性链表；而相应的非线性线性表有树、二叉树、图等等。

常见数据类型介绍：

数组：这个好理解，连续的嘛！一维数组，可以通过下标找到你，而且定义一个数组，在内存上是相邻的一块，非常符合线性表的概念。

栈：特殊一点，操作都在一端进行，这端或这头叫栈顶top，相反，另一端则为栈底bottom。如果为空的话叫空栈，特点就是：FILO(first in ,last out)

栈

  • 先进后出，后进先出
  • 插入删除操作都是在栈顶进行
  • 不像线性表，插入删除操作不需要移动栈内其他元素

插入栈内为入栈或压栈，退出为出栈或退栈，读取就是将栈顶元素读取。

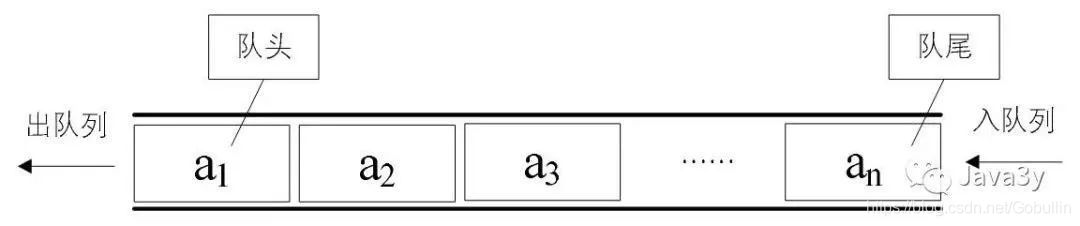
队列：一端插入，另一端退出删除。遵循FIFO，先进先出。那么哪里是头？哪里是尾呢？想象一下一列火车穿过隧道，火车头先进入隧道，然后尾部(Front)后进入。所以原理类似，在队尾(Rear)进行插入，在队头进行删除。

队列

树：非线性的，是可以分支和划分层次的，由n(n>=0)个结点构成，树的结点应该满足以下条件：

  • 只有一个没前驱的节点为根
  • 其余结点可以构成子树
  • 没有子结点的为叶子结点，其余为分支点或内点

一个结点的前件为父结点，后件为孩子结点，有子节点个数多少为度。结点中最大的度为树的度，最大的层数为树的深度。

二叉树：通常由一个结点和左右子树构成，每一个结点最多有两个子结点。

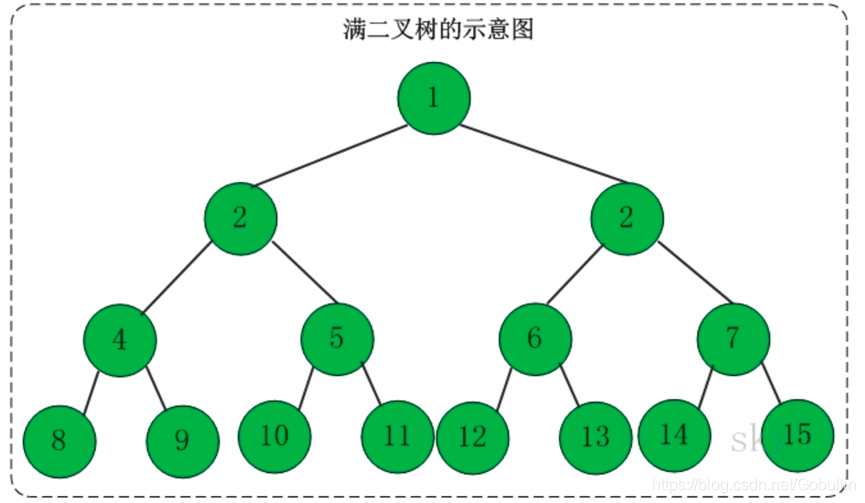
满二叉树：除最后一层外，每一层上的结点都有两个子节点，从第一层开始数到n层，第k层有2的n减一次方个结点，共2的n次方减一个结点。（国内是这么定义的，国外则不是，国外定义为一棵二叉树的结点要么是叶子结点，要么它有两个子结点）

国内：
满二叉树
国外：
国际二叉树

完全二叉树：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。 也就是说，满二叉树一定是完全二叉树！
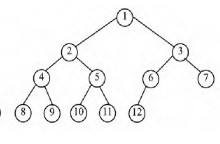
完全二叉树

完全二叉树的判定：

C++代码实现(不是本人亲写)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
#include <iostream>
#include <queue>
using namespace std;
 
template <class T>
struct TreeNode
{
    T data;
    TreeNode<T> *left;
    TreeNode<T> *right;
    TreeNode(const T &x) : data(x),
                           left(NULL),
                           right(NULL) {}
};
template <class T>
bool IsComplete(TreeNode<T> *root)
{
    //1.树为空，返回错误
    if (root == NULL) {
        return false;
    }
    //2.树不为空
    queue<TreeNode<T> *> q;
    q.push(root);
    while (!q.empty()){
        TreeNode<T> *top = q.front();
        //2.1如果该节点两个孩子都有，则直接pop
        if (top->left && top->right)  {
            q.pop();
            q.push(top->left);
            q.push(top->right);
        }
        //2.2如果该节点左孩子为空，右孩子不为空，则一定不是完全二叉树
        if (top->left == NULL && top->right   {
            return false;
        }
        //2.3如果该节点左孩子不为空，右孩子为空或者该节点为叶子节点，则该节点之后的所有结点都是叶子节点
        if ((top->left && top->right == NULL) || (top->left == NULL && top->right == NULL)) {
                      if (NULL != top->left && NULL == top->right)   {
                            q.push(top->left);    
                        }
            q.pop(); //则该节点之后的所有结点都是叶子节点
            while (!q.empty()) {
                top = q.front();
               if (top->left == NULL && top->right == NULL)  {
                    q.pop();
                }
                else  {
                    return false;
                }
            }
            return true;
        }												
    }															
    return true;
}															
//满二叉树
    //       1
    //   2       3
    // 4    5  6   7
void test1(){
    TreeNode<int> *node1 = new TreeNode<int>(1);
    TreeNode<int> *node2 = new TreeNode<int>(2);
    TreeNode<int> *node3 = new TreeNode<int>(3);
    TreeNode<int> *node4 = new TreeNode<int>(4);
    TreeNode<int> *node5 = new TreeNode<int>(5);
    TreeNode<int> *node6 = new TreeNode<int>(6);
    TreeNode<int> *node7 = new TreeNode<int>(7);
    node1->left = node2;
    node1->right = node3;
    node2->left = node4;
    node2->right = node5;
    node3->left = node6;
    node3->right = node7;
    cout << IsComplete<int>(node1) << endl;
} 
//二叉树为空
void test2(){
    cout << IsComplete<int>(NULL) << endl;
}
//3.二叉树不为空，也不是满二叉树，遇到一个结点左孩子为空，右孩子不为空
void test3(){
    //       1
    //   2       3
    // 4    5      7
    TreeNode<int> *node1 = new TreeNode<int>(1);
    TreeNode<int> *node2 = new TreeNode<int>(2);
    TreeNode<int> *node3 = new TreeNode<int>(3);
    TreeNode<int> *node4 = new TreeNode<int>(4);
    TreeNode<int> *node5 = new TreeNode<int>(5);
    TreeNode<int> *node7 = new TreeNode<int>(7);
    node1->left = node2;
    node1->right = node3;
    node2->left = node4;
    node2->right = node5;
    node3->right = node7;
    cout << IsComplete<int>(node1) << endl;
} 
//4.二叉树不为空，也不是满二叉树，遇到叶子节点,则该叶子节点之后的所有结点都为叶子节点
void test4(){
    //        1
    //    2       3
    // 4    5
    TreeNode<int> *node1 = new TreeNode<int>(1);
    TreeNode<int> *node2 = new TreeNode<int>(2);
    TreeNode<int> *node3 = new TreeNode<int>(3);
    TreeNode<int> *node4 = new TreeNode<int>(4);
    TreeNode<int> *node5 = new TreeNode<int>(5);
    node1->left = node2;
    node1->right = node3;
    node2->left = node4;
    node2->right = node5;
    cout << IsComplete<int>(node1) << endl;
}
//4.二叉树不为空，也不是满二叉树，遇到左孩子不为空，右孩子为空的结点，则该节点之后的所有结点都为叶子节点
void test5(){
    //        1
    //    2       3
    // 4    5   6
    TreeNode<int> *node1 = new TreeNode<int>(1);
    TreeNode<int> *node2 = new TreeNode<int>(2);
    TreeNode<int> *node3 = new TreeNode<int>(3);
    TreeNode<int> *node4 = new TreeNode<int>(4);
    TreeNode<int> *node5 = new TreeNode<int>(5);
    TreeNode<int> *node6 = new TreeNode<int>(6);
    node1->left = node2;
    node1->right = node3;
    node2->left = node4;
    node2->right = node5;
    node3->left = node6;
    cout << IsComplete<int>(node1) << endl;
}
int main(){
    test1();
    /*test2();*/
    /*test3();*/
    /*test4();*/
    /*test5();*/
    return 0;
}

源码连接：https://blog.csdn.net/gogogo_sky/article/details/76223384

二叉树通常用链式存储，每一个元素则可以有两个后件，分别可以指向左右子结点，其链式结构又叫二叉链表。

二叉树遍历：

二叉树遍历要求不能重复访问结点，常用的有前序遍历、中序遍历、后序遍历。

  • 前序遍历Data Left Right(DLR)：先访问根节点，然后遍历左子树，最后遍历右子树
  • 中序遍历Left Data Right(LDR)：先遍历左子树，访问根节点，最后遍历右子树
  • 后序遍历Left Right Data(LRD)：先遍历左子树，后遍历右子树，最后访问根节点

相应的文章请到博客园二叉树